Markowitz Modern Portfolio Theory

1. Theory

Modern portfolio theory (MPT), or mean-variance analysis, is a mathematical framework for assembling a portfolio of assets such that the expected return is maximized for a given level of risk. It uses the variance of asset prices as a proxy for risk.

Economist Harry Markowitz introduced MPT in a 1952 essay, for which he was later awarded a Nobel Prize in economics.

1.1 Multivariate Normal Distribution Assumption

The asset returns \(X = (X_1, X_2, ..., X_k)^T\) follow a multivariate normal distribution:

Each random variable follows a normal distribution: \(X_i\) ~ \(N(\mu_i, \sigma_i^2)\)

Mean vector \(\vec{\mu} = (E(X_1), E(X_2), ..., E(X_k))^T = (\mu_1, \mu_2, ..., \mu_k)^T\)

Covariance matrix \(\Sigma = \{ Cov[X_i, X_j] \} = \{ \rho_{ij} \sigma_i \sigma_j \}, (\rho_{ii}=1; i,j=1,2,...,k)\)

1.2 Mean-Variance optimization

• Allocation: portfolio weights for each asset \(\vec{w} = (w_1, w_2, ..., w_k)\).

• Portfolio mean (return) (reward):

  \(\mu_p = \vec{\mu}^T \vec{w}\)

• Portfolio variance (risk):

  \(\sigma_p^2 = \vec{w}^T \Sigma \vec{w}\)

• Optimization:

  \(\min_{\vec{w}} \{ Risk - \lambda * Reward \ | \ \vec{w} \in S \} \)

  • \(S\) is the feasible set;
  • \(\lambda \in [0, +\infty)\) represents the trade-off between reward and risk;
  • \(\lambda \to 0\): conservative manager who doesn't like any risk;
  • \(\lambda \to +\infty\): greedy manager who wants rewards as much as possible but doesn't care about risk.

• Standard form: quadratic optimization

  \(M = \min_\vec{w} ( \frac{1}{2}\vec{w}^T \Sigma \vec{w} - \lambda \vec{\mu}^T \vec{w} ) \)

  \(s.t. \sum{\vec{w}} = \vec{1}^{T} \vec{w} = 1 \)

• Lagrange multiplier: \(L(M) = \frac{1}{2}\vec{w}^T \Sigma \vec{w} - \lambda \vec{\mu}^T \vec{w} - \zeta (\vec{1}^T \vec{w} - 1) \)

  • Let the gradient be zero , then we can get the solution:
    • \(\nabla L(M) = \Sigma \vec{w} - \lambda \vec{\mu} - \zeta \vec{1} = 0 \)

       

      \( \vec{w} = \lambda \Sigma^{-1} \vec{\mu} + \zeta \Sigma^{-1} \vec{1} \)

  • Let \(\lambda\) be fixed, substitute the above solution in the constraint to get the Lagrange multiplier:

    \( \zeta = \frac{1-\lambda \vec{1} \Sigma^{-1} \vec{\mu}}{\vec{1} \Sigma^{-1} \vec{1}} \)

  • Then substitute it into the solution for \(\vec{w}\), we get the efficient frontier parameterized by \(\lambda\):

    \(\vec{w} = \lambda \Sigma^{-1} \mu + \left( \frac{1-\lambda \vec{1} \Sigma^{-1} \vec{\mu}}{\vec{1} \Sigma^{-1} \vec{1}} \right) \Sigma^{-1} \vec{1} \)

    • If \(\lambda = 0\), we get the Minimum Variance Portfolio:

      \(\vec{w} = \frac{\Sigma^{-1}\vec{1}}{\vec{1}^T \Sigma^{-1} \vec{1}} \)

  • Efficient frontier (or portfolio frontier) is an investment portfolio which occupies the 'efficient' parts of the risk-return spectrum.

1.3 References

https://en.wikipedia.org/wiki/Modern_portfolio_theory

https://en.wikipedia.org/wiki/Efficient_frontier

2. Practice

2.1 Two assets case

# cases of two assets

def plot_2s(r=[0.1, 0.15], s=[0.28, 0.24], cor=-0.1, cstr='r', lstr='-', 
            w=np.array([np.linspace(1,0,100), np.linspace(0,1,100)])):
    pr = np.dot(np.array(r).reshape([1,2]), w)[0]
    cormat = np.array([[s[0]*s[0], cor*s[0]*s[1]], [cor*s[0]*s[1], s[1]*s[1]]])
    ps = np.sqrt( np.sum(w * np.dot(cormat, w), axis=0) )
    plt.plot(s, r, cstr+'o')
    plt.plot(ps, pr, cstr+lstr)
    return pr, ps

plt.figure(1, figsize=(6,4))
cors = np.linspace(-1,1,11)
#cors = [0]
for cor in cors:
    cstr = ''
    if np.abs(cor+1) < 1e-6: cstr='r'
    if np.abs(cor-1) < 1e-6: cstr='b'
    if np.abs(cor-0) < 1e-6: cstr='k'
    pr, ps = plot_2s(r=[0.1, 0.15], s=[0.15, 0.25], cor=cor, cstr=cstr)
    imins = np.argmin(ps)
    plt.plot(ps[imins], pr[imins], cstr+'o')

plt.xlabel('risk: $\sigma_p$')
plt.ylabel('return: $\mu_p$')
plt.show()

As shown in the above figure, the smaller the correlation coefficients between two assets, the less risk we can get by choosing the weights of positions properly. If these two assets are negatively correlated, we can even get non-risk positive return (red dot). If they are positively correlated (blue line), the return and risk have a trivial linear relationship: the higher risk, the higher return.

2.2 Three assets case (general case)

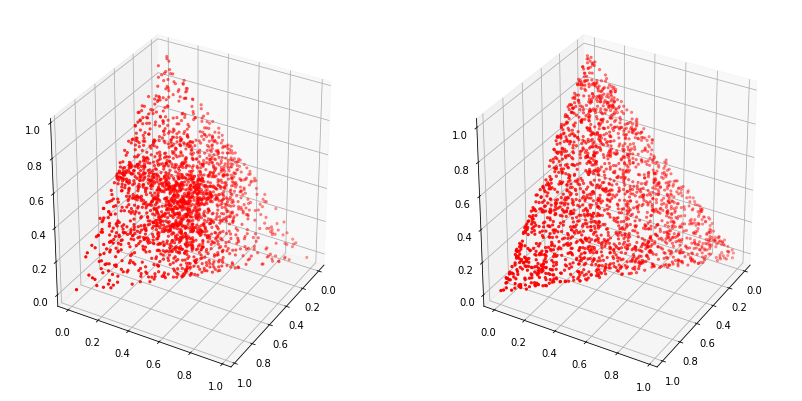
In this case, we need an uniform sampling method from the 3D space with constraint, which results in the Symmetric Dirichlet distribution

from mpl_toolkits.mplot3d import Axes3D

def sampling_weight(nx=3, nsp=10, flag=1):
    # uniform distributed samping with constrain: sum(x) = 1
    # nx: number of random variables
    # nsp: number of sampling points

    if flag==0:
        # Naive normalized method: NOT uniformly distributed on the simplex
        p = np.random.uniform(low=0, high=1, size=nx*nsp).reshape(nsp, nx)
        p = p / np.sum(p, axis=1).reshape(nsp,1)

    if flag==1:
        # Symmetric Dirichlet distribution: uniformly distributed on the simplex
        p = np.random.exponential(scale=1, size=nx*nsp).reshape(nsp, nx)
        p = p / np.sum(p, axis=1).reshape(nsp,1)

    return p 

plt.figure(1, figsize=(14,7))
for i in range(2):
    ax = plt.subplot(1,2,i+1, projection='3d')
    p = sampling_weight(nx=3, nsp=2000, flag=i)
    ax.scatter(p[:,0], p[:,1], p[:,2], c='r', s=20, marker='.')
    ax.view_init(30, 30)

# Case of multiple assets
import quadprog

def quadprog_solve_qp(P, q, G=None, h=None, A=None, b=None):
    qp_G = .5 * (P + P.T)   # make sure P is symmetric
    qp_a = -q
    qp_C = -np.vstack([A, G]).T
    qp_b = -np.hstack([b, h])    
    meq = A.shape[0]
    # print(qp_G.shape, qp_a.shape, qp_C.shape, qp_b.shape)
    return quadprog.solve_qp(qp_G, qp_a, qp_C, qp_b, meq)[0]

def port_retrisk(r0, cov, w):
    n = cov.shape[0]
    r = r0.reshape([n, 1])
    pr = np.dot(r.T, w.T)[0]
    ps = np.sqrt( np.sum(w.T * np.dot(cov, w.T), axis=0)  )
    return pr, ps

def minvarport(cov):
    n = cov.shape[0]
    u = np.ones([n]).reshape([n,1])
    cinv = np.linalg.inv(cov)
    return np.dot(u.T, cinv) / np.dot(np.dot(u.T, cinv), u)

def effrontier(r0, cov, lam=np.linspace(0,1,11), flag=1, upb=1.0, lowb=0.0):
    n = cov.shape[0]
    r = r0.reshape([n, 1])
    efw = np.zeros([len(lam), n])  # weights
    efp = np.zeros([len(lam), 2])  # [return, std]
    u = np.ones([n]).reshape([n,1])

    # analytical solution
    if flag == 1:
        cinv = np.linalg.inv(cov)
        for i in range(len(lam)):
            zeta = (1 - lam[i]*np.dot(u.T, np.dot(cinv, r))[0]) / np.sum(cinv, axis=(0,1))
            efw[i,:] = lam[i]*np.dot(cinv, r).reshape([1,n]) + \
                zeta[0] * np.sum(cinv, axis=1).reshape([1,n])
        efp[:,0], efp[:,1] = port_retrisk(r, cov, efw)

    # use quadratic programming library
    if flag == 2:
        for i in range(len(lam)):
            efw[i,:] = quadprog_solve_qp(cov, -lam[i]*r[:,0], \
                G = np.append( np.identity(n), -np.identity(n), axis=0), \
                h = np.append( upb+np.zeros(n), -lowb+np.zeros(n) ), \
                A = u.T, b=1.0 )
        efp[:,0], efp[:,1] = port_retrisk(r, cov, efw)

    return efw, efp


r = np.array([0.1, 0.15, 0.2])
s = np.array([0.28, 0.24, 0.25])
cor = np.array([[1, -0.1, 0.25], 
                [-0.1, 1, 0.20], 
                [0.25, 0.20, 1]])
cov = cor * (np.dot(s.reshape([3,1]), s.reshape([3,1]).T))

plt.figure(figsize=(10,8))

# Monte-Carlo simulation
w = sampling_weight(nx=3, nsp=2000, flag=1)
pr, ps = port_retrisk(r, cov, w)
flag = np.argmax(w, axis=1)
cstr = list('myc')
for i in range(3):
    plt.plot(ps[flag==i], pr[flag==i], cstr[i]+'.')

# Minimum variance portfolio
wmvp = minvarport(cov)
print('Analytical MVP =', wmvp[0])
print('Sample MVP =', w[np.argmin(ps),:])
r_mvp, s_mvp = port_retrisk(r, cov, wmvp)
plt.plot( s_mvp, r_mvp, 'ks')

# Efficient frontier
lam = np.linspace(0, 0.7, 8)  # Lagrange multiplier
efw, efp = effrontier(r, cov, lam=lam, flag=1)
plt.plot( efp[:,1], efp[:,0], 'ko')

# Efficient frontier
lam = np.linspace(0, 0.7, 8) + 0.05  # Lagrange multiplier
efw, efp = effrontier(r, cov, lam=lam, flag=2, upb=1.0)
plt.plot( efp[:,1], efp[:,0], 'ro')
efw, efp = effrontier(r, cov, lam=lam, flag=2, upb=0.8)
plt.plot( efp[:,1], efp[:,0], 'm+-')
efw, efp = effrontier(r, cov, lam=lam, flag=2, upb=0.6)
plt.plot( efp[:,1], efp[:,0], 'b+-')


# Every Pair
i=0; j=1; pr, ps = plot_2s(r=[r[i], r[j]], s=[s[i], s[j]], cor=cor[i,j], cstr='r')
i=0; j=2; pr, ps = plot_2s(r=[r[i], r[j]], s=[s[i], s[j]], cor=cor[i,j], cstr='g')
i=1; j=2; pr, ps = plot_2s(r=[r[i], r[j]], s=[s[i], s[j]], cor=cor[i,j], cstr='b')

plt.xlabel('risk: $\sigma_p$')
plt.ylabel('return: $\mu_p$')
plt.show()

Output:

Analytical MVP = [0.31596552 0.43908872 0.24494576]
Sample MVP = [0.30714531 0.42729323 0.26556146]

By comparing the above two figures, we will find that the portfolio return-risk map is simply a projection of the sampling domain of the weights of positions.